马考勒久期的计算公式
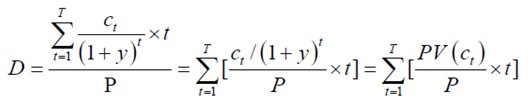
![MacD=\frac{\sum_{t=1}^T PV(c_t)\times t}{P}=\sum_{t=1}^T[\frac{PV(c_t)}{P}\times t]](https://wiki.mbalib.com/w/images/math/1/5/e/15e569d6a15bea19c72448931376c522.png)
(公式1)
其中,
MacD是马考勒久期,
P是债券当前的市场价格,
PV(Ct)是债券未来第t期可现金流(利息或资本)的现值,
T是债券的到期时间。
t为从当前到t时刻现金流发生的持续时间。
y为债券的风险程度相适应的收益率。假设未来所有现金流的贴现率都固定为y。

需要指出的是在债券发行时以及发行后,都可以计算马考勒久期。计算发行时的马考勒久期,T(到期时间)等于债券的期限;计算发行后的马考勒久期,T(到期时间)小于债券的期限。
马考勒久期定理
1.只有贴现债券的马考勒久期等于它们的到期时间
2.直接债券的马考勒久期小于或等于它们的到期时间
3.统一公债的马考勒久期等于[1+1/Y] ,其中Y是计算现值采用的贴现率
马考勒久期与债券价格的关系
对于给定的收益率变动幅度,马考勒久期越大,债券价格的波动幅度越大:
到期时间、息票率、到期收益率是决定债券价格的关键因素,与久期存在以下的关系:
1.零息票债券的久期等于到它的到期时间。
2.到期日不变,债券的久期随息票据利率的降低而延长。
3.息票据利率不变,债券的久期随到期时间的增加而增加。
4.其他因素不变,债券的到期收益率较低时,息票债券的久期较长。